Study on the efficiency and temperature robustness of chirped PPLN crystal in 1064nm frequency doubling experiment - 03

2. Theoretical analysis

2.2 Design of CPPLN crystal structure

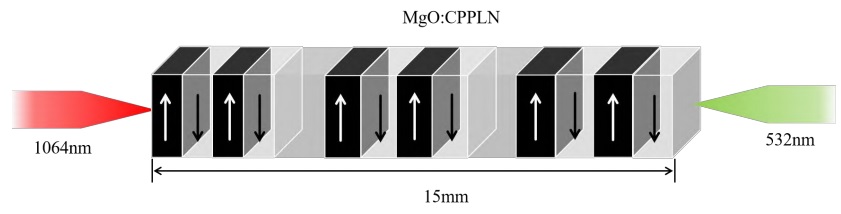
In order to achieve better temperature robustness and higher frequency doubling efficiency on the same CPPLN crystal, we designed the crystal structure of CPPLN. The schematic diagram of CPPLN for frequency doubling from 1064nm to 532nm is shown in Figure 1. The incident beam with fundamental frequency is set to be e-light, that is, its polarization direction is horizontal. At the same time, the output beam is also set to be e-light. This setting allows us to use the direction with the largest second-order nonlinear coefficient in the CPPLN crystal (d₃₃=27.2 pm/V).

Figure 1. Schematic diagram of CPPLN SHG process

The goal of this experiment is to improve the generation efficiency and stability of 532nm laser beam. Therefore, the gain bandwidth should be selected according to the possible temperature range. The smaller the better, to ensure that a higher frequency doubling efficiency can be obtained. The 1064nm light source used in this experiment is a self-built LD-pumped Nd:YVO₄ continuous laser. We first conducted a bandwidth test on this 1064nm laser beam and found it to be slightly less than 1nm. Considering the need to retain a certain margin, we set the gain bandwidth of the crystal to be 1nm. According to Formula 4, the initial period of CPPLN is selected as 6.99 μm, the chirp is 0.21 μm^-2, the number of periods is 2104, and the duty cycle is 49.61%. For the CPPLN crystal, its effective Fourier coefficient can be expressed in the reciprocal lattice vector domain as (Formula 5):

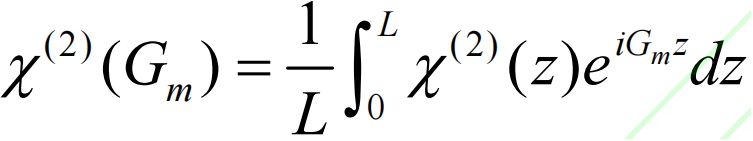
In order to intuitively see the performance of the CPPLN of this design structure, we use the above Formula 5 to perform Fourier transformation on the distribution of χ⁽²⁾ (z) of this structure, and obtain the effective Fourier coefficient of the CPPLN structure with respect to the reciprocal lattice vector distribution (as shown in Figure 2), and also put the relationship between temperature and the corresponding phase mismatch Δk in Figure 2 for comparative analysis. In Figure 2, T1 and T2 are at the two ends of the convex part of the refractive index curve, corresponding to the reciprocal lattice vectors that can compensate for the phase mismatch at temperatures of 13.84℃ and 27.24℃ respectively. Figure 2 shows that the reciprocal lattice vector provided by the CPPLN crystal of this structure can compensate for the phase mismatch in the range of 13.84℃ to 27.24℃, that is, within this temperature range, the frequency-doubled light output by the CPPLN will always be maintained at a high level.

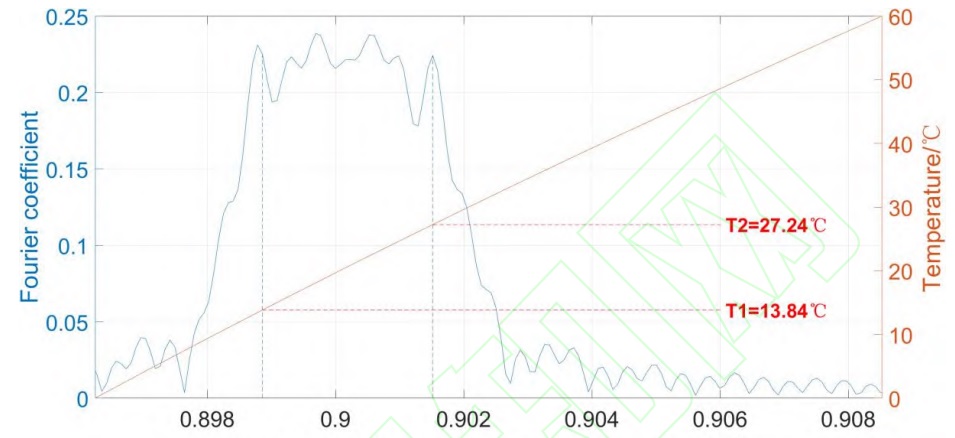
Figure 2. Reciprocal lattice vector / Phase mismatch (μm^-1)

From Formula 1, we can know that the main reason for the different frequency doubling efficiencies of frequency doubling crystals made from different materials is the difference in the refractive index for the fundamental light and the frequency doubling light and the difference in the effective nonlinear coefficient of the crystal itself. According to the Sellmeier equation, we can calculate the refractive index of 1064nm and 532nm light in CPPLN crystal and LBO crystal respectively as n_1,CPPLN = 2.1483, n_2,CPPLN = 2.2246, n_1,LBO = 1.6053, n_2,LBO = 1.6054. According to Figure 2, using the relationship d_eff,CPPLN = χ⁽²⁾ (G_m)*d₃₃, we can obtain the effective nonlinear coefficient of the designed CPPLN under quasi-phase matching conditions as d_eff,CPPLN = 6.46pm/V. The effective nonlinear coefficient of LBO can be calculated by software SNLO as d_eff,LBO = 0.83pm/V. Calculation shows that under ideal conditions, the frequency doubling efficiency of CPPLN will be significantly higher than that of LBO, reaching 24.47 times that of LBO.